Will this patern continue?
It is tempting to guess that it will, but this is only a guess.
Mathematicians call such gueses conjectures.
Thus, we have the following two conjectures.
What thoses ?
Dua Conjecture tersebut adalah
Conjecture 1
Diberikan bilangan bulat n > 1 dan n bilangan prima. Maka 2n -1 adalah bilangan prima
Conjecture 2
Diberikan bilangan bulat n > 1 dan n bukan bilangan prima. Maka 2n -1 adalah bukan bilangan prima
Bukti:
Conjecture 1
Secara kebetulan, ambil n = 11 (bilangan prima) maka 2n – 1 = 23 x 89 (bukan bilangan prima), jadi konjektur 1 dapat dipatahkan. Jadi konjektur 1 dapat dibuktikan merupakan perkiraan yang salah.
Dan bukti itu hanya dengan memberikan satu contoh saja, bukti seperti ini disebut bukti dengan kontra contoh (counter example)
Conjecture 2
Misal n bukan bilangan prima, a dan b bilangan bulat dimana 1 < a < n dan 1 < b < n dan n = ab. Misalkan x = 2b – 1 dan y = 1 + 2b + 22b + … + 2(a – 1)b. Maka
xy = 2ab – 1 = 2n – 1
Jadi 2n – 1 dapat dinyatakan menjadi perkalian dua bilangan bulat positif lebih dari 1, dengan demikian bukan bilangan prima
Diberikan dua buah pernyataan A dan B, setiap pernyataan mempunyai nilai benar saja atau salah saja. Masalah mendasar yang menjadi perhatian matematika adalah untuk memperlihatkan bahwa jika A pernyataan yang benar, maka B merupakan pernyataan yang benar.
Apakah pernyataan berikut ini benar?
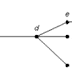
a. Kedudukan dua garis yang berbeda pada bidang adalah sejajar atau berpotongan.
b. 1 = 0
c. 3x = 5 atau y = 1
d. x adalah tidak lebih besar dari 0
e. Ada suatu sudut t sedemikian hingga cos t = t
Sumber : PPT Materi Pembelajaran Membaca dan Membuktikan dalam Matematika STKIP Garut
It is tempting to guess that it will, but this is only a guess.
Mathematicians call such gueses conjectures.
Thus, we have the following two conjectures.
What thoses ?
Dua Conjecture tersebut adalah
Conjecture 1
Diberikan bilangan bulat n > 1 dan n bilangan prima. Maka 2n -1 adalah bilangan prima
Conjecture 2
Diberikan bilangan bulat n > 1 dan n bukan bilangan prima. Maka 2n -1 adalah bukan bilangan prima
Bukti:
Conjecture 1
Secara kebetulan, ambil n = 11 (bilangan prima) maka 2n – 1 = 23 x 89 (bukan bilangan prima), jadi konjektur 1 dapat dipatahkan. Jadi konjektur 1 dapat dibuktikan merupakan perkiraan yang salah.
Dan bukti itu hanya dengan memberikan satu contoh saja, bukti seperti ini disebut bukti dengan kontra contoh (counter example)
Conjecture 2
Misal n bukan bilangan prima, a dan b bilangan bulat dimana 1 < a < n dan 1 < b < n dan n = ab. Misalkan x = 2b – 1 dan y = 1 + 2b + 22b + … + 2(a – 1)b. Maka
xy = 2ab – 1 = 2n – 1
Jadi 2n – 1 dapat dinyatakan menjadi perkalian dua bilangan bulat positif lebih dari 1, dengan demikian bukan bilangan prima
Diberikan dua buah pernyataan A dan B, setiap pernyataan mempunyai nilai benar saja atau salah saja. Masalah mendasar yang menjadi perhatian matematika adalah untuk memperlihatkan bahwa jika A pernyataan yang benar, maka B merupakan pernyataan yang benar.
Apakah pernyataan berikut ini benar?
a. Kedudukan dua garis yang berbeda pada bidang adalah sejajar atau berpotongan.
b. 1 = 0
c. 3x = 5 atau y = 1
d. x adalah tidak lebih besar dari 0
e. Ada suatu sudut t sedemikian hingga cos t = t
Sumber : PPT Materi Pembelajaran Membaca dan Membuktikan dalam Matematika STKIP Garut





No comments:
Post a Comment