A. Apa itu Eliminasi Gauss-Jordan

Eliminasi Gauss-Jordan merupakan cara eliminasi dengan mereduksi matriks menjadi bentuk eleson baris terreduksi.

Contoh Barisan Eselon Terreduksi
Biasanya Eliminasi Gauss / Gauss-Jordan ini digunakan untuk memecahkan sistem persamaan linear yang kemudian diubah kedalam bentuk matriks.
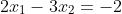
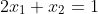

Jawab :
Matriks yang diperbesar untuk sistem tersebut adalah (langkah 1)

Kalikanlah baris pertama dengan 1/2 untuk mendapatkan 1 utama pada baris pertama (langkah 2)

Tambahkanlah -3 kali baris pertama pada baris ketiga (langkah 4)

Kalikanlah baris kedua dengan 1/4 untuk mendapatkan 1 utama pada baris kedua (langkah 5)

Tambahkanlah -13/2 kali baris pertama pada baris ketiga (langkah 6)

Kalikan baris ketiga dengan -8/7 untuk mendapatkan 1 utama pada baris ketiga (langkah 7)


Pemecahannya :
$x_1\,\, \, \, \, \, \, \, \, \, \, \, \, \, \, = \frac{1}{8}$
$\, \, \, x_2\, \, \, \, \, \, \, \, \, \, \, \,=\frac{3}{4}$
Eliminasi Gauss-Jordan merupakan cara eliminasi dengan mereduksi matriks menjadi bentuk eleson baris terreduksi.
Contoh Barisan Eselon Terreduksi
Biasanya Eliminasi Gauss / Gauss-Jordan ini digunakan untuk memecahkan sistem persamaan linear yang kemudian diubah kedalam bentuk matriks.
Contoh :
Pecahkanlah sistem berikut dengan menggunakan eliminasi Gauss-Jordan!
Jawab :
Matriks yang diperbesar untuk sistem tersebut adalah (langkah 1)
Kalikanlah baris pertama dengan 1/2 untuk mendapatkan 1 utama pada baris pertama (langkah 2)
Tambahkanlah -2 kali baris pertama pada baris kedua (langkah 3)
Tambahkanlah -3 kali baris pertama pada baris ketiga (langkah 4)
Kalikanlah baris kedua dengan 1/4 untuk mendapatkan 1 utama pada baris kedua (langkah 5)
Tambahkanlah -13/2 kali baris pertama pada baris ketiga (langkah 6)
Kalikan baris ketiga dengan -8/7 untuk mendapatkan 1 utama pada baris ketiga (langkah 7)

Tambahkanlah 3/2 kali baris kedua pada baris pertama (langkah 8)
Pemecahannya :
$x_1\,\, \, \, \, \, \, \, \, \, \, \, \, \, \, = \frac{1}{8}$
$\, \, \, x_2\, \, \, \, \, \, \, \, \, \, \, \,=\frac{3}{4}$

.png)








No comments:
Post a Comment