Di dalam kombinatorial, kita harus menhitung (counting) semua kemungkinan pengaturan objek. Dua kaidah dasar yang digunakan sebagai teknik menghitung dalam kombinatorial adalah kaidah perkalian (rule of product) dan kaidah penjumlahan (rule of sum). Kedua kaidah ini dapat digunakan untuk memecahkan banyak masalah persoalan menghitung.
a. Kaidah Perkalian (rule of product)
Bila percobaan 1 mempunyai p hasil percobaan yang mungkin terjadi (atau menghasilkan p kemungkinan jawaban), percobaan 2 mempunyai q hasil percobaan yang mungkin terjadi (atau menghasilkan q kemungkinan jawaban), maka bila percobaan 1 dan percobaan 2 dilakukan maka terdapat hasil percobaan (atau menghasilkan kemungkinan jawaban).
b. Kaidah Penjumlahan (rule of sum)
Bila percobaan 1 mempunyai p hasil percobaan yang mungkin terjadi (atau menghasilkan p kemungkinan jawaban), percobaan 2 mempunyai q hasil percobaan yang mungkin terjadi (atau menghasilkan q kemungkinan jawaban), maka bila hanya satu percobaan saja yang dilakukan (percobaan 1 atau percobaan 2), terdapat p + q kemungkinan hasil percobaan (menghasilkan p + q kemungkinan jawaban) yang mungkin terjadi.
Perhatikanlah kata yang digaris bawahi pada kedua diatas: dan serta atau. Kedua kata ini adalah kata kunci untuk mengidentifikasi apakah suatu persoalan menghitung diselesaikan dengan kaidah perkalian atau kaidah penjumlahan. Kaidah perkalian menyatakan bahwa kedua percobaan dilakukan secara simultan atau serempak, sedangkan pada kaidah penjumlahan, kedua percobaan dilakukan tidak simultan.
Contoh 1.1 sampai 1.2 berikut memperlihatkan penggunaan kaidah perkalian dan kaidah penjumlahan untuk menghitung pengaturan objek-objek. Kita harus dapat menganalisis kapan menggunakan kaidah perkalian dan kaidah penjumlahan.
Contoh 1.1 :
Sebuah restoran menyediakan lima jenis makanan, misalnya nasi goring, roti, soto ayam, sate dan sop. Serta tiga jenis minuman, misalnya susu, kopi dan teh. Jika setiap orang boleh memesan satu makanan dan satu minuman, berapa banyak pasangan makanan dan minuman yang dapat dipesan?
Penyelesaian:
Kita data menggunakan diagram pohon untuk menentukan jumlah pasangan makanan dan minuman yang dapat dipesan. Pada diagram pohon tersebut, akar adalah awal pemilihan, cabang adalah alternative solusi dan daun merupakan akhir solusi.
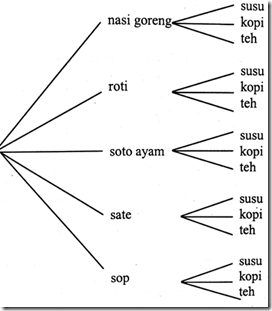
Berdasarkan diagram pohon diatas, kita mengenumerasi semua kemungkinan pasangan makanan dan minuman yang dapat dipesan, yaitu:
Semuanya ada 15 pasang.
Dalam kombinatorial, kita memandang bahwa dalam kejadian ini orang harus memilih makanan dan minuman. Ada 5 kemungkinan memilih makanan, yaitu nasi goreng, roti, soto ayam , sate dan sop. Ada 3 kemungkinan memilih minuman yaitu susu, kopi dan teh, sehingga dengan menggunakan kaidah perkalian, jumlah kemungkinan pasangan makanan dan minuman yang dapat dipesan adalah pasang.
Contoh 1.2 :
Jabatan ketua himpunan dapat diduduki oleh mahasiswa angkatan tahun 1997 atau angkatan tahun 1998. Jika terdapat 45 orang mahasiswa angkatan 1997 dan 52 orang mahasiswa angkatan 1998, berapa cara memilih pejabat ketua himpunan?
Penyelesaian :
Jabatan yang ditawarkan hanya ada satu, yang dapat diduduki oleh salah seorang mahasiswa dari dua angkatan yang ada. Ada 45 cara memilih satu orang mahasiswa dari Angkatan 1997, dan 52 cara memilih satu orang dari angkatan 1998, namun hanya satu dari kedua angkatan itu yang terpilih (angkatan 1997 atau angkatan 1998). Dalam kombinatorial, dari kedua kejadian, hanya satu dari dua kejadian yang dilakukan, sehingga dengan menggunakan kaidah penjumlahan, jumlah cara memilih pejabat ketua himpunan tersebut sama dengan jumlah mahasiswa pada kedua angkatan, yaitu 45 + 52 = 97 cara.
Sumber : Rinaldi Munir + Catatan
a. Kaidah Perkalian (rule of product)
Bila percobaan 1 mempunyai p hasil percobaan yang mungkin terjadi (atau menghasilkan p kemungkinan jawaban), percobaan 2 mempunyai q hasil percobaan yang mungkin terjadi (atau menghasilkan q kemungkinan jawaban), maka bila percobaan 1 dan percobaan 2 dilakukan maka terdapat hasil percobaan (atau menghasilkan kemungkinan jawaban).
b. Kaidah Penjumlahan (rule of sum)
Bila percobaan 1 mempunyai p hasil percobaan yang mungkin terjadi (atau menghasilkan p kemungkinan jawaban), percobaan 2 mempunyai q hasil percobaan yang mungkin terjadi (atau menghasilkan q kemungkinan jawaban), maka bila hanya satu percobaan saja yang dilakukan (percobaan 1 atau percobaan 2), terdapat p + q kemungkinan hasil percobaan (menghasilkan p + q kemungkinan jawaban) yang mungkin terjadi.
Perhatikanlah kata yang digaris bawahi pada kedua diatas: dan serta atau. Kedua kata ini adalah kata kunci untuk mengidentifikasi apakah suatu persoalan menghitung diselesaikan dengan kaidah perkalian atau kaidah penjumlahan. Kaidah perkalian menyatakan bahwa kedua percobaan dilakukan secara simultan atau serempak, sedangkan pada kaidah penjumlahan, kedua percobaan dilakukan tidak simultan.
Contoh 1.1 sampai 1.2 berikut memperlihatkan penggunaan kaidah perkalian dan kaidah penjumlahan untuk menghitung pengaturan objek-objek. Kita harus dapat menganalisis kapan menggunakan kaidah perkalian dan kaidah penjumlahan.
Contoh 1.1 :
Sebuah restoran menyediakan lima jenis makanan, misalnya nasi goring, roti, soto ayam, sate dan sop. Serta tiga jenis minuman, misalnya susu, kopi dan teh. Jika setiap orang boleh memesan satu makanan dan satu minuman, berapa banyak pasangan makanan dan minuman yang dapat dipesan?
Penyelesaian:
Kita data menggunakan diagram pohon untuk menentukan jumlah pasangan makanan dan minuman yang dapat dipesan. Pada diagram pohon tersebut, akar adalah awal pemilihan, cabang adalah alternative solusi dan daun merupakan akhir solusi.

Berdasarkan diagram pohon diatas, kita mengenumerasi semua kemungkinan pasangan makanan dan minuman yang dapat dipesan, yaitu:
Nasi goreng dan susu
Nasi goreng dan kopi
Nasi goreng dan teh
Roti dan susu
Roti dan kopi
Roti dan teh
Soto ayam dan susu
Soto ayam dan kopi
|
Soto ayam dan teh
Sate dan susu
Sate dan kopi
Sate dan teh
Sop dan susu
Sop dan kopi
Sop dan teh
|
Dalam kombinatorial, kita memandang bahwa dalam kejadian ini orang harus memilih makanan dan minuman. Ada 5 kemungkinan memilih makanan, yaitu nasi goreng, roti, soto ayam , sate dan sop. Ada 3 kemungkinan memilih minuman yaitu susu, kopi dan teh, sehingga dengan menggunakan kaidah perkalian, jumlah kemungkinan pasangan makanan dan minuman yang dapat dipesan adalah pasang.
Contoh 1.2 :
Jabatan ketua himpunan dapat diduduki oleh mahasiswa angkatan tahun 1997 atau angkatan tahun 1998. Jika terdapat 45 orang mahasiswa angkatan 1997 dan 52 orang mahasiswa angkatan 1998, berapa cara memilih pejabat ketua himpunan?
Penyelesaian :
Jabatan yang ditawarkan hanya ada satu, yang dapat diduduki oleh salah seorang mahasiswa dari dua angkatan yang ada. Ada 45 cara memilih satu orang mahasiswa dari Angkatan 1997, dan 52 cara memilih satu orang dari angkatan 1998, namun hanya satu dari kedua angkatan itu yang terpilih (angkatan 1997 atau angkatan 1998). Dalam kombinatorial, dari kedua kejadian, hanya satu dari dua kejadian yang dilakukan, sehingga dengan menggunakan kaidah penjumlahan, jumlah cara memilih pejabat ketua himpunan tersebut sama dengan jumlah mahasiswa pada kedua angkatan, yaitu 45 + 52 = 97 cara.
Sumber : Rinaldi Munir + Catatan


No comments:
Post a Comment